SolarPVBasic1, SolarPVBasic2
Weather Related Models were added in Version 23
There are several Power Flow Weather Models that can be used to make a weather/time/location dependent MWMax for a solar PV generator.
The concepts for this model are discussed in detail in Chapter 4 of the book “Renewable and Efficient Electric Power Systems, 2nd Edition”, Gilbert M. Masters, ISBN: 978-1-118-63350-2, May 2013 Wiley-IEEE Press, 720 Pages
Model Inputs
|
Inputs |
Description |
|
DateTime |
The date and time of a simulation is important for solar PV plants. When using the time-step simulation tool this will manage this. Otherwise a global case time can is specified at the top of the Case Description dialog. |
|
Latitude and Longitude |
Latitude and Longitude location is obtained from the generator object. The latitude and longitude are specified either with the terminal bus of the generator or with the Substation object to which the terminal bus is assigned. |
|
CloudCoverPerc |
The CloudCoverPerc will be obtained from the generator field WS_CloudCoverPerc as described in the help topic Generator assignments to WeatherStation and XYCurve. If this is not available there will be an input parameter with the model for DefaultCloudCoverPerc. |
Parameters for SolarPVBasic1 and SolarPVBasic2.
|
Parameter |
Description |
|
AllowTurnOff |
Set to 1 to indicate that if a software tool results in an output = 0, then the generator can be turned off (status set to OPEN). For any value other than 1, then the generator will not be opened automatically by this model. |
|
AllowTurnOn |
Set to 1 to indicate that if a software tool results in an output > 0, then the generator can be turned on (status set to CLOSED). For any value other than 1, then the generator will not be closed automatically by this model. |
|
Tracking |
Integer code indicating if any solar tracking is used. 0 = None 1 = Single Axis with Fixed Tilt Angle 2 = Single Axis with Fixed Azimuth 3 = Dual Axis |
|
MWMax |
The MW output of the solar panels at the Latitude of the generator when operating on the summer solstice (June 21 in Northern hemisphere) at solar noon and also assuming that the panels are facing directly at the sun. This means that for this model, MWMax will only be reached if the Dual Axis Tracking available. |
|
AzimuthDeg |
AzimuthDeg is only used if operating at a fixed Azimuth. (Tracking = 0 or 2). Azimuth is the angle between compass South and the direction normal to the plane of the solar panel) |
|
TiltOffsetDeg or TiltAngleDeg
TiltAngleUsed |
Tilt parameters are only used if operating at a fixed Tilt Angle (Tracking = 0 or 1). The solar panel tilt is the angle between the vertical and a vector normal to the plane of the solar panel. For SolarPVBasic1, the input parameter is TiltOffsetDeg and it represent the offset from the latitude. For SolarPVBasic1: TiltAngleUsed = Latitude + TiltOffsetDeg For SolarPVBasic2: TiltAngleUsed = TiltAngleDeg For purposes of Diffuse Energy, if Tracking=0 or 1 then TiltAngleUsed = ElevationSolar |
|
DiffuseFactor |
A fraction between 0.0 and 1.00 representing the fraction of the solar energy reaching the earth that does not come from direct sunlight. It’s the energy that is scattered (or diffused) by the atmosphere but still reaches the surface of the earth. This portion of the energy reaching the surface of the earth is not impacted by cloud cover and all the various angles and factors. |
|
DefaultCloud |
Normally, this model obtains the value of CloudCoverPerc from the value WM_CloudCoverPerc of the generator object which obtains it from the associated WeatherStation object. If there is no valid WeatherStation associated with the generator, then the model parameter DefaultCloud is used instead. |
The Solar PV models also make an assumption that the angle between the Earth's rotational axis and the orbital axis is 23.45 degrees. The tropic of Cancer is defined at Latitude = +23.45 degrees and the Tropic of Capricorn is defined at Latitude -23.45 degrees.
To calculate the normalized MW output of the Solar PV Panel, the following calculations must be done
Declination Angle (DeclinationSolar)
Declination angle is the angle between the rays of the Sun and the plane of the Earth's equator. We define the angle as -23.45 degrees on December 21. We then define the N to represent the day of the year with N=0 representing January 1 at 12:00 AM and N=365 representing December 31 at midnight. The declanation angle is then defined as
DeclinationSolar = -23.45*cos( 360/365 * (N+10) )
All angles are expressed in degrees. The "+10" exists because the winter solstice occurs 10 days before January 1.
Solar Hour Angle (HRA)
The solar hour angle represents the time of day at the present location as an angle in degrees. The angle 0.0 degrees is defined as the moment when the sun is highest in the sky at that latitude and longitude. This is "solar time" and will not match the local clock time which is defined by local time zones. Each hour of the day then represents 15 degrees (15*24 = 360) . The Hour Angle is going to be impacted by the Longitude of the location.
Solar Elevation Angle (ElevationSolar)
Solar Elevation Angle is also called the Solar Altitude Angle. It is the angle between the horizontal and the sun representing how high in the sky the sun is. It is calculated using the following equation.
ElevationSolar= arcsin( sin(DeclinationSolar)*sin(Latitude) + cos(DeclinationSolar)*cos(Latitude)*cos(HRA) )
The maximum solar elevation will occur when HRA = 0 (at noon), so cos(HRA) = 1. Using the trigonometric identities that cos(A-B) = sin(A)sin(B) + cos(A)cos(B) and cos(A) = sin(A+90) will give that ElevationMax = Declination - Latitude+ 90. There are some differences when LAT is negative so the actual equation becomes
If Latitude>= 0 then ElevationSolarMax = DeclinationSolar - Latitude+ 90 Else ElevationSolarMax = -DeclinationSolar + Latitude+ 90
Finally, we don't want ElevationMax > 90 (which can occur inside the tropics), so if
If ElevationSolarMax > 90 then ElevationSolarMax = 180 - ElevationSolarMax
Solar Azimuth Angle (AzimuthSolar)
Solar azimuth angle is defined as the angle between the projection of sun’s center onto the horizontal plane and the due South direction. If DeclinationSolar < 90, then we calculate the azimuth angle as
AzimuthSolar=arctan2[-cos(DeclinationSolar)* sin(HRA), sin(DeclinationSolar)*cos(Latitude) - cos(HRA)*cos(DeclinationSolar)*sin(Latitude) ]
Finally, we define Solar Azimuth as an angle between 0 and 360 degrees, so also check
If AzimuthSolar<0 then AzimuthSolar=AzimuthSolar+360
Atmospheric Transmittance (Transmittance)
Atmospheric transmittance is a measure of what fraction of the energy survives a trip through the atmosphere. This is discussed on pages 213 – 215 of the Master's book. Atmospheric transmittance is a function of the distance of the atmosphere that the solar energy must travel though and thus is a function of the solar elevation angle (α_s). It is also a function of many factors that are very hard to quantify such as dust, air pollution, water vapor, and turbidity. For our simple solar models for use in power system studies, we will make no attempt to quantify these and will us an exponential decay function: T=Ae^(-km)
The parameter A is a value in W/m^2 and represents the apparent solar energy in outer space. The parameters k is called the optical depth. For our basic model the value of A is not important because it will cancel out in our approximation and for the value of k we will use 0.197. The parameter m represents the air mass ratio which represents the total amount of air the solar energy traverses to get from outer space to the solar panel, relative to the amount that traverses to the solar panel if the sun was directly overhead (ElevationSolar=90 degrees). The empirically determined Equation (4.21) on page 215 of the Master’s book is m=((708 sin(ElevationSolar) )^2+1417)^0.5 - 708 sin(ElevationSolar).
This gives a value of Atmospheric Transmittance of
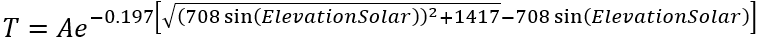
For a given latitude, we then calculate the maximum value of Solar Transmittance possible. This will occur on the summer solstice at noon and the value of ElevationSolar = 90+23.45 - abs(LAT) at that time for latitudes outside of the tropics. For latitudes inside the tropics use ElevationSolar = 90 instead which will make the entire term in square brackets equal to 1.0. This will give a normalized Atmospheric Transmittance of the following withe the A terms canceling out because of the division.

PV Tracking and Direct Solar Energy
The final amount of direct beam energy reaching the solar panel is effected by the type of solar panel tracking available. We assume the solar panels are a flat surface.
If the solar panel has a fixed Azimuth Angle (the angle between South and the compass direction normal to the plane of the solar panel), then the factor Kaz will be applied
Kaz=cos(AzimuthDeg - AzimuthSolar)
Where AzimuthDeg is a model parameter and AzimuthSolar is the angle calculated as described above.
If the solar panel tilt angle (angle between the vertical and vector normal to the plane of the solar panel), the factor Ktilt will be applied.
Ktilt=cos(90-TiltAngleUsed-ElevationSolar)
Where ElevationSolar is the angle between the horizontal plane and the direction of the sun calculated as described above.
Solar PV Tracking can be applied to track the East to West movement of the sun (Azimuth tracking) and/or to track the up and down movement of the sun (Tilt Tracking). The user input code Tracking is an integer 0, 1, 2 or 3 to signify this and the treatment is as follows
Tracking = 0 means there is no PV Tracking and thus Kaz=cos(AzimuthDeg - AzimuthSolar) and Ktilt=cos(90-TiltAngleUsed-ElevationSolar)
Tracking = 1 means there is single axis PV Tracking with a Fixed Tilt Angle thus Kaz=1.0 and Ktilt=cos(90-TiltAngleUsed-ElevationSolar)
Tracking = 2 means there is single axis PV Tracking with a Fixed Azimuth thus Kaz=cos(AzimuthDeg - AzimuthSolar) and Ktilt=1.0
Tracking = 3 means there is dual axis PV Tracking so Kaz=1.0 and Ktilt=1.0
Diffuse Solar Energy
The equations above have all discussed the geometry around direct beam radiation from the sun to the panel. Not all the energy from the sun arrives this way however. Diffused radiation is the energy that is scattered (or diffused) by the atmosphere but reaches the surface of the earth in a randomized way from all angles. This portion of the energy reaching the surface of the earth is not impacted by the various angles and factors discussed above. The portion of the diffuse energy that reaches the solar panel however is a function of what proportion of the sky that the panel sees. If the panel is pointed directly upwards then it sees "all of the sky", however if it is tiled vertically then it only sees 50% of the sky. In the extreme if it were oriented downward (pointing at the ground) it would see none of this diffuse energy. The Diffuse Energy reaching the panel will be proportional to the function (1 + sin(TiltAngleUsed))/2
Reflected Solar Energy
The Master's book also discusses solar energy that is reflected off other surfaces on page 220. The simple models we are showing here ignore this source of energy.
Normalized Power Reaching the Solar Panel
The model input parameter DiffuseFactor represents the fraction of the solar energy reaching the earth as Diffuse Energy. Another input to this model will be CloudCoverPerc equal to the generator's field WM_CloudCoverPerc which obtains it from the associated WeatherStation object. If there is no valid WeatherStation associated with the generator, then the model parameter DefaultCloud is used instead. The final model Normalized Output Scalar is then calculated as follows.

This normalized value is then multiplied by the model parameter MWMax to create the output of the solar PV model which represents the weather-dependent MWMax value that should be used by the generator. Finally depending on the input parameters AllowTurnOff and AllowTurnOn the model may also either open or close the generator described in the logic below.
Output (new MWMax)=OutScalar*MWMax
